Fraction Addition and Subtraction and Mixed Number Notation

Addition and Subtraction Rule

In summary, to add or subtract fractions, it is sufficient to change the fractions so that they have common denominators. Then we add or subtract the numerators and keep the common denominator. Finally, we simplify that answer, if it is not already in simplest form.

 

Here is an example adding more than two fractions at a time. Find the sum .

 

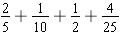First, find the least common multiple of denominators. This will give us the least common denominator. We find LCM (5, 10, 2, 25) by the prime factorization method.

 5 = 5,  10 = 2 ∙ 5,  2 = 2, and  25 = 5²

So the LCM (5, 10, 2, 25) = 2 ∙ 5² = 2 ∙ 25 = 50

We now change each addend to fractions with the common denominator.

Note that we simplified  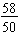and then changed it to a mixed number. A more detailed illustration follows where we show each step: first simplify the fraction, then since the fraction is an improper fraction, split the improper fraction into a whole and a fractional part, and then write as a mixed number.

This answer, 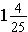, is a mixed number.  Any improper fraction can be also be expressed as a mixed number because there is more than one whole in the improper fraction.

 

return to top | previous page | next page