Introduction to Probability

Experimental and Theoretical Probability

Probability is the mathematics of chance. Probability is used to describe the predictable long-run patterns of random outcomes. For instance, if you toss a fair coin a single time, the outcome (heads or tails) is completely random and unpredictable. But if a coin is tossed 10,000 times, we would expect that the coin would come up heads approximately half the time.

To start calculating probabilities, we begin with equally likely outcomes. For instance, when tossing a fair coin, a head and a tail are equally likely outcomes. When tossing a standard die each of the six sides is equally likely to show.

When we discuss probability in mathematics, we often perform or study probability experiments. Keeping track of the results from tossing a coin to determine the probability of a single flip would be an example of a probability experiment. Also, a probability experiment could be performed by tossing a standard die or pair of dice.

When we actually perform the experiment to see what happens, we get an experimental probability. For instance, John Kerrich (1903–1985) as a prisoner of war during World War II performed the probability experiment of tossing a coin 10,000 times and recording whether it landed heads or tails. He obtained 5067 heads. So the experimental probability of getting heads for his experiment was 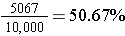. Though after 100 tosses, he had obtained only 44 heads. If he had stopped at that point, his experimental probability for a head would have been

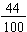 or 44%. For more information on John Kerrich or his experiment, see A Brief History of the School of Statistics - University of the Witwatersrand and http://www.wiley.com/college/stat/wild329363/pdf/ch_04.pdf.

Another type of probability that is usable for some types of problems where we do not actually need to perform an experiment is theoretical probability.The theoretical probability of getting heads on a toss of a fair coin is  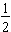because there is only one way to get heads out of two equally likely ways for the coin to land. This same type of thinking can be expanded to cover a number of probability situations. But first we need to define some basic terms used in the study of probability.

return to top | previous page | next page