Introduction to Probability

Some Basic Definitions for Probability

Sample Space: In probability, the set of all possible outcomes is called the Sample Space. We will use S to represent the sample space. In terms of the language of sets, a sample space is a universal set and an outcome is an element of the universal set.

Example: The sample space for the experiment of toss a coin once would be
S = {H, T} because there are only two possible outcomes, Heads or Tails.

Notice that we frequently abbreviate the outcomes when listing them.

Example: The sample space for the experiment of a toss a standard die would be:
S = {1, 2, 3, 4, 5, 6} because these are the only six possible outcomes.

Event: In probability, an event is a subset of the sample space. In a probability experiment, the event for which we wish to compute the probability is called the target event.

Example: If we want to compute the probability of obtaining a head when tossing a fair coin, then "obtaining a head" is the event. Note that {H} is a subset of S = {H, T}. Also, P(H) represents the probability of obtaining a head.

Example: If we want to compute the probability of getting a 3 or 4 when tossing a standard die, then "getting a 3 or 4" is the target event. Note that E = {3, 4} is a subset of S = {1, 2, 3, 4, 5, 6}. Also, P(E) is the notation that stands for the probability of event E occurring.

For an experiment in which all outcomes are equally likely, the probability of an event E is computed by finding the ratio of the number of elements in the target event E to the number of elements in the sample space S. In the context of probability, we write ratios in their fraction form.

Example: The event of obtaining a 3 or 4 in the experiment of a toss of a standard die is E = {3, 4}. The sample space for the experiment of a toss a standard die is
S = {1, 2, 3, 4, 5, 6}.
So, .

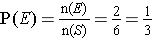Remember that n(E) is the cardinal number of the set of events and n(S) is the cardinal number of the sample space.

Example: What is the probability of getting an even number when a fair, 6-sided die is rolled? Express this probability as a percent.

First we determine the sample space. Since a fair 6-sided die only has the numbers 1, 2, 3, 4, 5, and 6 as possibilities, and each is as likely to happen as the other, the sample space S = {1, 2, 3, 4, 5, 6} consists of equally likely outcomes.

Then we need to determine the target event set. In this case we want even numbers that can occur on a 6-sided die. Thus our event E = {2, 4, 6}.
So, 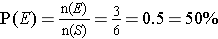. The probability of obtaining an even number when a fair standard die is tossed is 50%.

Self-Check Problems

Five names (Dana, Jamie, Lynn, Pat, and Shawn) are put in a hat where one name is to be randomly drawn for a door prize.

What is the sample space?

What is the event where either Dana or Pat's name is drawn?

What is the probability of the event where either Dana or Pat's name is drawn?

Solutions

return to top | previous page | next page