Department of Technology

ENG 200 - Surveying

E-mail Me

All My Webs

Dept Home

Coordinate Operations

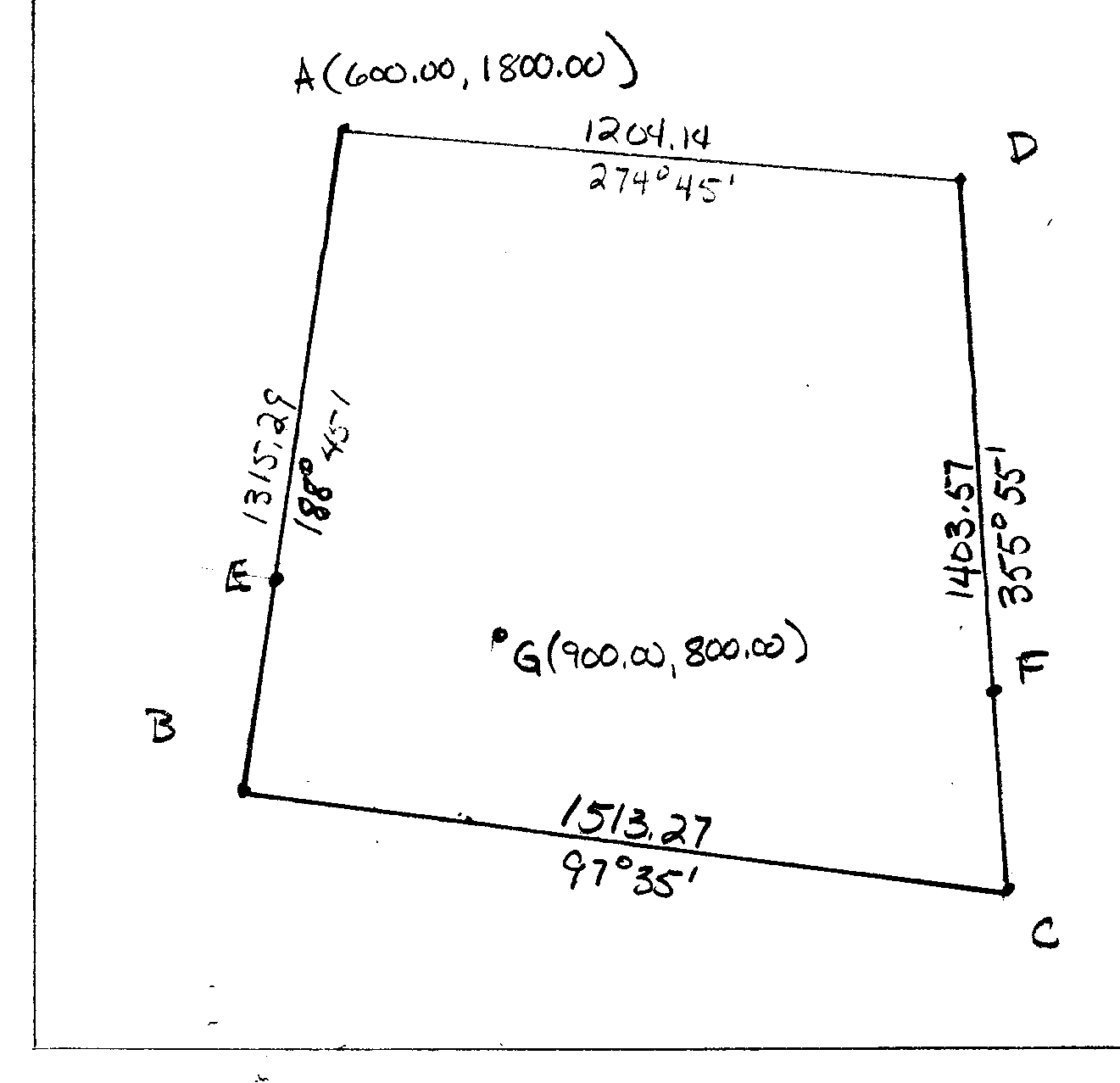
Recall from Chapter 11 some key facts about coordinates:

• The origin point is selected arbitrarily so that the coordinates of one point are known, and so that the coordinates of all the other points are positive values.  In the figure below, the origin was set so that the coordinates of A are X_A = 600.00 and Y_A = 1800.00.
  

• The coordinates of subsequent points around the traverse are found from the following:

  • X_B = X_A + Dep_AB

  • Y_B = Y_A + Lat_AB
    

• If the coordinates of two points are known, the equations above will yield:

  • Dep_AB  = X_B + X_A

  • Lat_AB  = Y_B + Y_A

  • Length_AB  = (Lat_AB^² + Dep_AB^²)^{^1/2}

  • Azimuth_AB  = ArcTan(Dep_AB/Lat_AB)

Most of the relationships between points are based on two general concepts:

• Any two points can be connected by a line.  The equation for that line can be written in the form
  Y = mX + b, where m represents the slope of the line and b is the Y-intercept.  Given the coordinates of two points, A and B, the equation can be found from these formulae:

  • m_AB = (Lat_AB/Dep_AB) = 1/Tan(Azimuth_AB)

  • b_AB = Y_A - X_A(m_AB)

  For the figure above, m_AB = 1/Tan(188°45') = 6.4971,
  and b_AB = 1800.00 - 600.00(6.4971) = -2098.26,
  so the equation for line AB is Y = 6.4971X - 2098.26.
  

• The coordinates of a point where two lines intersect must satisfy the equation for both lines.  For example if the equation for line BC is Y = -0.13314X +553.25, there will be only one point, B, where Y_B = -0.13314X_B + 553.25 and Y_B = 6.4971X_B - 2098.26.  By setting the right sides of both equations equal, and solving for the X coordinate, the general form of the equation would be:
            X = -(b_B - b_A)/(m_B - m_A)
  Y could then be found by plugging X into either of the line equations.

Two other concepts are also useful in defining point/line relationships: 

• Parallel line have the same slope, but different intercepts. 

• Perpendicular lines have inverse slopes, but the sign changes.  For example, if the slope of line AB is known to be  m = 6.4971, the slope of a line perpendicular to it will be -1/6.4971 = -0.1539.

The attached Excel file uses these equations to:

1. Define the coordinates for a point E, 900 feet from A, along line AB.

2. Define the equation for a line parallel to BC, passing through E.

3. Define the coordinates for a point F where the line through E intersects with CD.

4. Define the equation of a line perpendicular to BC and passing through G.

5. Define the coordinates of the point where that line intersects BC.

6. Determine the length of the perpendicular line from G to line BC.