Exponents
Definition of an Exponent: The expression 
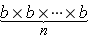 , which is n factors of b used for n – 1 multiplications, can be written as bn. The b is called the base and the n is called the exponent.
, which is n factors of b used for n – 1 multiplications, can be written as bn. The b is called the base and the n is called the exponent.
Examples:
- A coin is flipped three times. How many outcomes are possible?
To solve the above problem in Session 9 (Old Session 9), we completed a tree diagram (as illustrated below) to solve the problem to motivate the Fundamental Counting Principle.
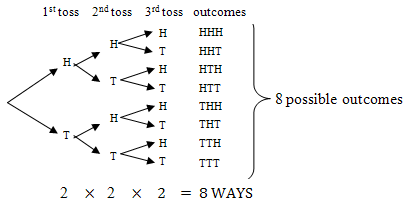
Note that we could also express the problem in exponential form as
23 = 2 × 2 × 2 = 8.
We have eight possible outcomes when a coin is flipped three times.
- What if we were to flip a coin four times? How many outcomes are possible?
Setting up the problem using exponents, we obtain 24 = 2 × 2 × 2 × 2 = 16. There would be sixteen possible outcomes if a coin is flipped four times.
- If we flip the coin thirteen times, then 213 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 8,192. We would have 8,192 different possible outcomes if a coin is flipped thirteen times.
Note that as the number of times we have to repeat the multiplication becomes larger, the notation of using only multiplication becomes cumbersome. So, we use the short-cut notation with exponents to represent this type of repeated multiplication.
Example: In 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2, the 2 is repeated 13 times.

More Examples:
- 32 = 3 × 3 = 9
- Use repeated multiplication to find 53, 105, and 93.
53 = 5 × 5 × 5 = 25 × 5 = 125
105 = 10 × 10 × 10 × 10 × 10 = 100,000
93 = 9 × 9 × 9 = 9 × 81 = 729
- Dino is eating at his favorite Italian restaurant. On the menu there are three wines, three salads, three entrees, and three desserts. There are also three credit cards in his wallet. How many ways can he choose a meal choosing exactly one of each type of item and pay fo it with a credit card?
We apply the Fundamental Counting Principle and use exponents to obtain
and use exponents to obtain
35 = 3 × 3 × 3 × 3 × 3 = 243.
Dino has 243 choices for a meal and paying for it.
Self-Check Problem
A standard die is rolled five times. How many outcomes are possible? Write the problem in exponential form and then solve it.
Solution
return to top | previous page | next page


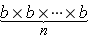 , which is n factors of b used for n – 1 multiplications, can be written as bn. The b is called the base and the n is called the exponent.
, which is n factors of b used for n – 1 multiplications, can be written as bn. The b is called the base and the n is called the exponent.
 and use exponents to obtain
and use exponents to obtain