Exponents and Simplifying Expressions

Multiplying Variable Expressions

Previously we learned to add variable expressions by adding like terms. Now that we have exponents, we can also multiply variable expressions. First we note that x · x = x² since the variable x has been used as a factor twice. This is just applying the definition of an exponent. Similarly, we have that a · a · a · a · a · a = a ⁶.

Now consider 3x(2x). Since everything in this expression is multiplied, we use the commutative and associative properties of multiplication with the definition of exponent to find the product:

Example: Multiply (4x)(2x)(x).

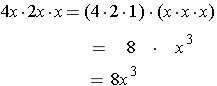
Example: Multiply (3x)(y)(x²)(5y).

Notice that coefficients are grouped together and then each different variable is grouped together.

 We note that we only add like terms and obtain like terms. But when we multiply expression with variables we do not obtain like terms , instead we get expressions with exponents. It is important to learn to make this distinction when simplifying variable expressions.

Compare each of the following when adding or multiplying the same terms.

Addition	Multiplication
2x + 3x = (2 + 3)x = 5x	2x · 3x = (2 · 3)x = 6x
4y + y + 2y = (4 + 1 + 2)y = 7y	4y · y · 2y = (4 · 1 · 2)(y · y · y) = 8y3
a + 2b + a + b = a + a + 2b + b = 2a + 3b	a · 2b · a · b = 2 · a · a · b · b = 2a2b2

Self-Check Problems

Evaluate each expression:

4m + 5n + m + 7n + 2m and 4m · 5n · m · 7n · 2m

Solutions

return to top | previous page | next page