4.7.3 Tangent Lines to Point Conics  Printout
"For example," is not a proof.
—Jewish Proverb

Definition. A tangent to a point conic is a line that has exactly one point in common with the point conic.

        Do tangents to a point conic exist? If a tangent exists at a point of a point conic, is it unique? These are the first questions we need to address. Click here to explore the first question with a dynamic sketch GeoGebra or JavaSketchpad.
        Remember, from the definition of point conic, that a point is in a point conic if it is a point of intersection of corresponding lines in two projectively, but not perspectively, related pencils of lines.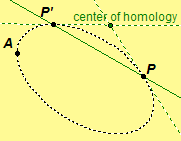 Also, any pair of points in the point conic may be chosen as the centers for two projectively related pencils of lines defining the point conic. Let P  be any point of a point conic and P' be another point of the point conic. There must be a line l through P that is projectively related to the line PP'. (Note that l must pass through the center of homology as in the dual of the proof of Theorem 4.15.) We assert that l is tangent to the point conic at P. If not, then there is a point A in the point conic such that A is on l and A is distinct from P. Then PA = l  is projectively related to P'A. Thus, l is projectively related to both P'P and P'A, which contradicts that projectivities are one-to-one mappings. Hence, l is a tangent to the point conic at P. Similarly, there is a tangent to the point conic at P'. We have answered the first question and proven the following theorem.

Theorem 4.22. There exists a tangent at every point of a point conic. Further, the lines corresponding to the common line of the projectivity determining a point conic are tangents.

        Continue the above argument. Suppose there is a second tangent line m to the point conic at P. Since m is in the pencil of points with center P, by the projectivity, there exists a corresponding line m' in the pencil of points with center P'. Then P = m · m', since the intersection of m and m' is a point in the point conic and m is tangent to the point conic at P. Thus m' = PP'. Hence, l and m are both projectively related to PP', a contradiction. Therefore, l is the unique line tangent to the point conic at P. Hence, the line tangent to a point conic at a point is unique. We have proven the following theorem.

Theorem 4.23. The tangent line at any point of a point conic is unique.

        Now we are ready to justify our conjecture based on the investigation at the end of the page on Pascal's Theorem. We conjecture the next theorem. Our investigation illustrated that the result is a degenerate case of Pascal's Theorem.

Theorem 4.24. If A, B, C, D, and E are five distinct points of a point conic, then the three points AB · DE, BC · EA, and CD · (tangent at A) are collinear.

        Note the saying at the top of this page, "For example, is not a proof." Our investigation is not a proof. Our investigation seemed to imply that we could prove the theorem by taking the limit as F tends to A to form a degenerate case of Pascal's Theorem. But this limit process fails to prove the result for three reasons:

• It has not been shown there are more than finitely many points in a projective plane.

• There is no axiom of continuity. The points of a point conic may be discrete and not contiguous.

• No axiom implies that every point in a projective plane is a limit point.

Proof. Let A, B, C, D, and E be five distinct points of a point conic. Let l be the tangent to the point conic at A. Let I = AB · DE, J = EA · BC, and K = l · CD. We need to show that I, J, and K are collinear. Let K' = IJ · CD. The lines K'A and l are either the same line or distinct lines.
        Suppose K'A and l are distinct. Note K'A is not tangent to the point conic since l is the unique line tangent to the conic at A. Hence, there is a point F in the point conic such that F is on K'A and is not A. Now, F is either distinct from or is one of B, C, D, and E.
        Case 1. Assume F is distinct from B, C, D, and E. By Pascal's Theorem, I = AB · DE, J' = EF · BC, and K' = AF · CD are collinear. Note J and J' are distinct. (Why are J and J' distinct points?) Since {I, J, K'} and {I, J', K'} are collinear sets, {I, J, J', K'} is collinear. Thus, since {J, B, C} and {J', B, C} are collinear sets, {I, J, J', K', B, C} is collinear. Hence, since {K', C, D} is a collinear set, {I, J, J', K', B, C, D} is collinear. But this contradicts that B, C, and D are noncollinear since any three distinct points of a point conic are noncollinear.
        Case 2. Assume F = B. Note the sets {A, B = F, K'}, {A, B = F, I}, {I, J, K'}, and {J, B = F, C} are collinear. Hence, {A, B = F, C, I, J, K'} is collinear. But this contradicts that A, B, and C are noncollinear.
        The arguments for the other cases are similar, all leading to a contradiction. Since all the cases lead to a contradiction, we must have K'A = l.
        By how K and K' were defined, K = l · CD = K'A · CD = K'. Hence, since K = K' = IJ · CD, we must have I, J, and K collinear.//

        The above proof is clearly not very "elegant", but it does avoid the traps in writing an incorrect proof by depending on a picture or by making additional assumptions as stated in the comments before the proof.

Theorem 4.25. A line intersects a point conic in at most two points.

Exercise 4.51. Complete the case where F = C in the proof of Theorem 4.24.

Exercise 4.52. Given five points of a point conic, construct the tangent to one of the points by construction of the projectivity as in the proof of Theorem 4.22. (May use dynamic geometry software.)

Exercise 4.53. Given five points of a point conic, construct the tangent to one of the points applying Theorem 4.24 (the degenerate form of Pascal's Theorem.) (May use dynamic geometry software.)

Exercise 4.54. Prove Theorem 4.25.