TOC & Ch. 0 & Ch. 1 Axiom Table of Contents Ch. 0 Introduction Ch. 1 Axiomatic Systems 1.1.1 Introduction 1.1.2 Examples 1.1.3 History 1.2 A Finite Geometry 1.3 Finite Projective 1.4 Applications

Ch. 2 Neutral Geometry Ch. 2 Table of Contents 2.1.1 Introduction 2.1.2 History 2.1.3 Analytic Models 2.2 Incidence Axioms 2.3 Distance/Ruler Axioms 2.4.1 Plane Separation Axiom 2.4.2 Angle & Measure 2.5.1 Supplement Postulate 2.5.2 SAS Postulate 2.6.1 Parallel Lines 2.6.2 Saccheri Quadrilateral 2.7.1 Euclid Parallel Postulate 2.7.2 Hyperbolic Parallel Postulate 2.7.3 Elliptic Parallel Postulate 2.8 Euclid/Hyperbolic/Elliptic Birkhoff's Axioms Hilbert's Axioms SMSG Axioms

Ch. 3 Transformational Ch. 3 Table of Contents 3.1.1 Introduction 3.1.2 History 3.2.1 Definitions 3.2.2 Analytic Model 3.2.3 Affine Transformation 3.3.1 Isometry 3.3.2 Model/Collinearity 3.3.3 Model/Isometry 3.4.1 Direct Isometry 3.4.2 Model/Direct 3.5.1 Indirect Isometry 3.5.2 Model/Indirect 3.6.1 Similarity Transformation 3.6.2 Model/Similarity 3.7 Other Affine Transformations

Ch. 4 Projective Geometry Ch. 4 Table of Contents 4.1.1 Introduction 4.1.2 Historical 4.2.1 Axioms 4.2.2 Basic Theorems 4.3 Duality 4.4 Desargue's Theorem 4.5.1 Harmonic Sets 4.5.2 Music & Harmonic Sets 4.6.1 Definitions for Projectivity 4.6.2 Fundamental Theorem 4.6.3 Projectivity/Harmonic Sets 4.6.4 Alternate Construction 4.7.1 Conics 4.7.2 Pascal's Theorem 4.7.3 Tangents to Conics

Other Topics Ch. 5 Spherical Geometry Ch. 6 Fractal Geometry Ch. 7 Topology

Appendices Internet Resources Index Geometer's Sketchpad/GeoGebra JavaSketchpad/GeoGebraHTML Video Lectures Logic Review References Acknowledgements

4.6.4 Alternate Construction of a Projectivity  Printout
Mathematicians create by acts of insight and intuition. Logic then sanctions the conquests of intuition.
—Morris Kline (1908–1992)

        Here, we will formalize the definitions and results from the investigation on the previous page.

Definition. Given two distinct pencils of points with axes p and p', the points A, B  on p and corresponding points A', B' on p' determine lines AB' and BA' called cross joins.

Your exploration of the problem should have led to conjecturing the following theorem known as the Theorem of Pappus after Pappus of Alexandria (290-350).

Theorem 4.15. (Theorem of Pappus) A projectivity between two distinct pencils of points determines a line, which contains the intersection of the cross joins of any two pairs of corresponding points.

Proof.  Let p and p'  be the axes of two distinct projectively related  pencils of points. Assume P = p · p' and  such that P is none of the six points A, B, C, A', B', C'. Note the line AA' and the cross joins from A and A' determine two elementary correspondences  and . Since ,  and , we have . Since line AA' maps to itself through the projectivity, the dual of Corollary 4.12 implies that there exists a line 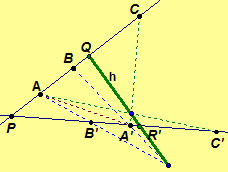h such that this projectivity is a perspectivity with axis h, , and does not depend on the choice of B and C. Hence, the intersection of the cross joins containing A and A', such as A'B · AB' and A'C · AC',  are on h.
        We need to show the line h is unique and contains the intersections of all pairs of cross joins . Since the above derivation of h used the line AA', we need to show that h is independent of this choice. That is, we need to show that the choice of BB', CC', or some other corresponding pair of points would determine the same line h.
        Assume h_x is determined from XX' where X and X' are corresponding points from the projectivity that are distinct from P. Since P is common to both pencils p and p', let Q be the pre-image of P, i.e., Q' = P, and let R' be the image of P under the projectivity, i.e., P = R. Thus,  X'Q · XQ' = X'Q · XP = Q and X'R · XR' = X'P · XR' = R'. Hence, Q and R' are on line h_x. If Q and R' are distinct, then h_x = QR' for any choice of XX'. If Q and R' are not distinct, then Q = R' = P. Let S = X'Y · XY' which is on lines determined from XX' and YY'. Hence, h_x = PS = h_y; that is, the determined line is the same line for any choice of XX' and YY'. By the Fundamental Theorem, the image and pre-image of P are unique; therefore, by both cases, h is uniquely determined by Q and R'.
        The projectivity determines a unique line h that contains the intersection of the cross joins of any two pairs of corresponding points.//

Definition. The line containing the intersections of the cross joins between the two pencils of points is called the axis of homology. The point containing the intersection of the lines determined by the cross joins between two pencils of lines is called the center of homology.

Exercise 4.39. Construct the axis of homology for two projectively related pencils of points. Then use the construction to determine an image of an arbitrary point.  (May use dynamic geometry software.)

Exercise 4.40. Construct the center of homology for two projectively related pencils of lines. Then use the construction to determine an image of an arbitrary line.  (May use dynamic geometry software.)