As an achievement it [Apollonius' Conic Sections] is so monumental that it practically closed the subject to later thinkers, at least from the purely geometrical standpoint.
—
4.7.1 Conics in the Projective Plane
![]() Printout
Printout
As an achievement it [Apollonius' Conic Sections] is so monumental that it
practically closed the subject to later thinkers, at least from the purely
geometrical standpoint.
—![]() Morris
Kline
(1908–1992)
Morris
Kline
(1908–1992)
The study of conics first arose
from the attempts to solve the problem of duplicating the cube, one of the three
famous problems from antiquity (![]() trisecting the angle,
trisecting the angle, ![]() duplicating the cube, and
duplicating the cube, and
![]() squaring the circle.) Two ancient stories are credited with the motivation
behind the problem of duplicating the cube. A Greek poet stated that the
mythological
squaring the circle.) Two ancient stories are credited with the motivation
behind the problem of duplicating the cube. A Greek poet stated that the
mythological ![]() King Minos desired the tomb of his son, Glaucus, be doubled in
size. The error by the poet was stating that this could be accomplished by
doubling each dimension. The later story is that the Athenians, in order to end a
plague (430 B.C.) which broke out during the war with Sparta, were instructed
by the oracle at
King Minos desired the tomb of his son, Glaucus, be doubled in
size. The error by the poet was stating that this could be accomplished by
doubling each dimension. The later story is that the Athenians, in order to end a
plague (430 B.C.) which broke out during the war with Sparta, were instructed
by the oracle at ![]() Delos to double the size of the cubical alter to Apollo.
Delos to double the size of the cubical alter to Apollo.
There are many definitions for conics. The definition used here is
credited to ![]() Jakob Steiner (1796–1867),
a Swiss mathematician.
Jakob Steiner (1796–1867),
a Swiss mathematician.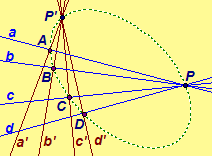
Definition. A point conic is the set of points of intersection of corresponding lines of two projectively, but not perspectively, related pencils of lines with distinct centers.
In the diagram on the
left, the two pencils of lines are projectively related.
Click here for a dynamic
illustration of a point conic and a line conic
GeoGebra or JavaSketchpad.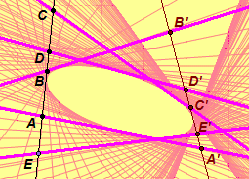 In the line conic, the ellipse or hyperbola is formed by the envelope of lines
determined from the projectively related pencils of points. See the adjacent
diagram on the right or investigate further by going to the
dynamic illustration of a point conic and
line conic GeoGebra or
JavaSketchpad.
In the line conic, the ellipse or hyperbola is formed by the envelope of lines
determined from the projectively related pencils of points. See the adjacent
diagram on the right or investigate further by going to the
dynamic illustration of a point conic and
line conic GeoGebra or
JavaSketchpad.
Definition. A line conic is the set of lines that join corresponding points of two projectively, but not perspectively, related pencils of points with distinct axes.
Note in each diagram (or from your investigation) how the centers/axes are
related to the point conic/line conic.![]() The centers of the pencil of lines appear
to be points of the point conic, and the axes of the pencil of points appear to
be lines in the line conic. We state and prove this conjecture with the next
theorem.
The centers of the pencil of lines appear
to be points of the point conic, and the axes of the pencil of points appear to
be lines in the line conic. We state and prove this conjecture with the next
theorem.
Theorem 4.16. The centers of the pencils of lines defining a point conic are points of the point conic.
Proof. Let P and P' be the centers of two
pencils of lines defining a point conic. Let p = PP'. Then p is a
line in the pencil with center P. Since the two pencils of lines are
projectively related, there is a line p' corresponding to p in the
pencil of lines with center P'. Since the pencils of lines are not
perspectively related, p and p' are distinct (Dual of
Corollary 4.12). Hence, by definition of point
conic, P' = p ·
p' is a point of the point conic.
The argument is the similar for
P. Let p' = PP' be a line in the pencil with center P'.
Thus, there is a distinct line p corresponding to p' in the pencil
of lines with center P. Hence, P = p
·
p' is a point of the point conic. Therefore, P and P' are both
points in the point conic.//
By the dual of the Fundamental Theorem, we know that a projectivity between two
pencils of lines is uniquely determined by three pairs of corresponding lines.
![]() Thus, the definition of a point conic implies that given any three pairs of
corresponding lines a unique projectivity is determined. Further, three
points of a point conic are also determined. Putting this observation with
Theorem 4.16, we easily
obtain five points of a point conic.
Thus, the definition of a point conic implies that given any three pairs of
corresponding lines a unique projectivity is determined. Further, three
points of a point conic are also determined. Putting this observation with
Theorem 4.16, we easily
obtain five points of a point conic.
A natural question arises: Do any
five points, where no three are collinear, determine a point conic? We
investigate the question by letting A, B, C, D, E be five distinct
points, no three of which are collinear. The lines AD, BD, CD and lines
AE, BE, CE are two pencils of lines with centers D and E,
respectively. By the dual of the Fundamental Theorem, there is a unique
projectivity between the two pencils of lines. Since A, B, and
C are intersections of corresponding lines and are noncollinear, the
projectivity is not a perspectivity. Hence, by the definition of a
point conic and Theorem 4.16, A, B, C, D, E are points of a
point conic. We have proven the following theorem.
Theorem 4.17. Any five distinct points, no three collinear, determine a point conic where two of the points are the centers of the respective pencils of lines.
Any two points may be chosen as the centers of the respective pencils. Do different choices for the centers give different point conics? That is, do any five points, no three collinear, determine a unique point conic?
Exercise 4.41. Construct the projectivity as a product of two perspectivities determined by a point conic formed from five points, no three collinear. Use the projectivity to construct a sixth point of the point conic. (May use dynamic geometry software.)
Exercise 4.42. Construct the projectivity by using the center of homology determined by a point conic formed from five points, no three collinear. Use the projectivity to construct a sixth point of the point conic. (May use dynamic geometry software.)
Exercise 4.43. (a) State the dual of Exercise 4.41 and perform the construction. (b) State the dual of Exercise 4.42 and perform the construction. (May use dynamic geometry software.)
Exercise 4.44. Prove that any three distinct points in a point conic are noncollinear.
Exercise 4.45. The definition of point conic includes the phrase "but not perspectively." If this phrase is omitted from the definition, the result would allow all of the points on two lines as points of the point conic. What two lines, defined by the perspectivity, would they be?
|
4.6.4 Alternate Construction of a Projectivity |
|
© Copyright 2005, 2006 - Timothy Peil |