TOC & Ch. 0 & Ch. 1 Axiom Table of Contents Ch. 0 Introduction Ch. 1 Axiomatic Systems 1.1.1 Introduction 1.1.2 Examples 1.1.3 History 1.2 A Finite Geometry 1.3 Finite Projective 1.4 Applications

Ch. 2 Neutral Geometry Ch. 2 Table of Contents 2.1.1 Introduction 2.1.2 History 2.1.3 Analytic Models 2.2 Incidence Axioms 2.3 Distance/Ruler Axioms 2.4.1 Plane Separation Axiom 2.4.2 Angle & Measure 2.5.1 Supplement Postulate 2.5.2 SAS Postulate 2.6.1 Parallel Lines 2.6.2 Saccheri Quadrilateral 2.7.1 Euclid Parallel Postulate 2.7.2 Hyperbolic Parallel Postulate 2.7.3 Elliptic Parallel Postulate 2.8 Euclid/Hyperbolic/Elliptic Birkhoff's Axioms Hilbert's Axioms SMSG Axioms

Ch. 3 Transformational Ch. 3 Table of Contents 3.1.1 Introduction 3.1.2 History 3.2.1 Definitions 3.2.2 Analytic Model 3.2.3 Affine Transformation 3.3.1 Isometry 3.3.2 Model/Collinearity 3.3.3 Model/Isometry 3.4.1 Direct Isometry 3.4.2 Model/Direct 3.5.1 Indirect Isometry 3.5.2 Model/Indirect 3.6.1 Similarity Transformation 3.6.2 Model/Similarity 3.7 Other Affine Transformations

Ch. 4 Projective Geometry Ch. 4 Table of Contents 4.1.1 Introduction 4.1.2 Historical 4.2.1 Axioms 4.2.2 Basic Theorems 4.3 Duality 4.4 Desargue's Theorem 4.5.1 Harmonic Sets 4.5.2 Music & Harmonic Sets 4.6.1 Definitions for Projectivity 4.6.2 Fundamental Theorem 4.6.3 Projectivity/Harmonic Sets 4.6.4 Alternate Construction 4.7.1 Conics 4.7.2 Pascal's Theorem 4.7.3 Tangents to Conics

Other Topics Ch. 5 Spherical Geometry Ch. 6 Fractal Geometry Ch. 7 Topology

Appendices Internet Resources Index Geometer's Sketchpad/GeoGebra JavaSketchpad/GeoGebraHTML Video Lectures Logic Review References Acknowledgements

             4.6.2 Fundamental Theorem of Projective Geometry  Printout
All truths are easy to understand once they are discovered; the point is to discover them..
—Galileo Galilei (1564–1643)

 

        In the introduction to projective geometry, we stated that in a later section we would consider a mapping between two pencils of points. We begin by showing that there exists a projectivity between two pencils of points. (The first video is the lecture and the second video is the construction in Geometer's Sketchpad.)
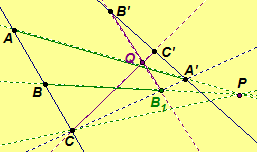
        Assume A, B, C are elements of a pencil with axis p and A', B', C' are elements of a pencil with axis p'.  Further, assume the points are distinct and the axes p and p' are distinct. We desire to find a projectivity so that ABC is projectively related to A'B'C', i.e. . Since a projectivity is a composition of perspectivities, we construct two perspectivities to map ABC to A'B'C'.

        To construct the first perspectivity, we define the center of a perspectivity that will map A to A' and C to itself with the image of B to be found. Let P be a point on AA' that is distinct from A and A'. (How do we know point P exists?) Let B₁ = BP · A'C. Thus .
     For the second perspectivity, we define the center of a perspectivity that maps A' to itself, B₁ to B', and C to C'. Let Q = B₁B' · CC'. Then . Since  and , we have . We have proven the following theorem.

 

Theorem 4.10. If A, B, C and A', B', C' are distinct elements in pencils of points with distinct axes p and p', respectively, then there exists a projectivity such that ABC is projectively related to A'B'C'.

 

        Further, the theorem and its constructive proof 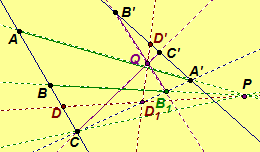give a procedure to determine a corresponding point D' on axis p' by following the perspectivities when a fourth point D on axis p is given. That is, let D be an element of axis p. First, find D₁ on the pencil of points with A', B₁, and C by mapping D through center P; that is, let D₁ = DP · A'C. Next, map D₁ to D' by mapping D₁ through the center Q to p', i.e., D' = D₁ Q · p'. Then  and . Hence, .

 

Exercise 4.30.  Show that P in the constructive proof of Theorem 4.10 exists.

 

Exercise 4.31. (a)  State and prove the dual of Theorem 4.10. (Hint: principle of duality)   (b)  Assume a, b, c are elements of a pencil with center P and a', b', c' are elements of a pencil with center P'. Use dynamic geometry software to construct and find a corresponding line d' of a line d.  (Hint: write the dual of the steps of the above construction for points.)

 

        In the above theorem, we have shown a projectivity exists between two pencils of points with three elements. But, is the projectivity unique? Since an arbitrary point was chosen in the construction, a different point would give different perspectivities. That is, would a different point  be determined, if the perspectivities were different? Click here to investigate the uniqueness of the perspectivity GeoGebra or JavaSketchpad constructed in the proof of the previous theorem. Also, to help answer these questions consider Axiom 6.

 

Axiom 6. If a projectivity on a pencil of points leaves three distinct points of the pencil invariant, it leaves every point of the pencil invariant.

 

      Axiom 6 implies that a projectivity on a pencil that leaves three elements of the pencil invariant is the identity mapping. What implications does this axiom have for distinct pencils of points? What implications does this axiom have for a projectivity on a pencil of points where no group of three points are mapped to themselves? Can this axiom extend the above theorem for constructing a projectivity between two pencils of points to more than three points? All of these questions are answered by the Fundamental Theorem of Projective Geometry, which has the surprising result that only three pairs of points are needed to determine a unique projectivity between two pencils of points.

 

Theorem 4.11. (Fundamental Theorem of Projective Geometry)  A projectivity between two pencils of points is uniquely determined by three pairs of corresponding points.

 

In other words, if A, B, C, D are in a pencil of points with axis p and A', B', C' are in a pencil of points with axis p', then there exists a unique point D'  on p' such that .

 

Proof.  Assume A, B, C, D are in a pencil of points with axis p and A', B', C' are in a pencil of points with axis p'. We have shown that there exists a point D' on p' such that . Suppose there is a projectivity and a point D" such that . Since  and , we have . Therefore, by Axiom 6, D' = D". //

 

        Note the principle of duality extends the fundamental theorem to pencils of lines. And it can easily be extended to where one set is a pencil of lines and the other is a pencil of points. , , and .

 

Corollary 4.12. A projectivity between two distinct pencils of points with a common element that corresponds to itself is a perspectivity.

 

Exercise 4.32. Given four collinear points A, B, C, D, use a dynamic geometry software to construct each projectivity and the image of the fourth point D. (For at least one of the exercises, you may need to draw another arbitrary pencil of points that is distinct from the given pencil of points.)

1.  
   
2.  
   
3.  
   

 

Exercise 4.33. Given four concurrent lines a, b, c, d, use a dynamic geometry software to construct each projectivity and the image of the fourth line d.

1.  
   
2.  
   
3.  
   

 

Exercise 4.34. Prove: Given three concurrent lines a, b, and c and two points P and Q not on any of the three lines. If A_i, and B_i are points on a and b, respectively, such that A_iP · B_iQ = C_i is on line c, then .

 

Exercise 4.35. Prove Corollary 4.12. (Remember a perspectivity is a projectivity, but a projectivity need not be a perspectivity.)