TOC & Ch. 0 & Ch. 1 Axiom Table of Contents Ch. 0 Introduction Ch. 1 Axiomatic Systems 1.1.1 Introduction 1.1.2 Examples 1.1.3 History 1.2 A Finite Geometry 1.3 Finite Projective 1.4 Applications

Ch. 2 Neutral Geometry Ch. 2 Table of Contents 2.1.1 Introduction 2.1.2 History 2.1.3 Analytic Models 2.2 Incidence Axioms 2.3 Distance/Ruler Axioms 2.4.1 Plane Separation Axiom 2.4.2 Angle & Measure 2.5.1 Supplement Postulate 2.5.2 SAS Postulate 2.6.1 Parallel Lines 2.6.2 Saccheri Quadrilateral 2.7.1 Euclid Parallel Postulate 2.7.2 Hyperbolic Parallel Postulate 2.7.3 Elliptic Parallel Postulate 2.8 Euclid/Hyperbolic/Elliptic Birkhoff's Axioms Hilbert's Axioms SMSG Axioms

Ch. 3 Transformational Ch. 3 Table of Contents 3.1.1 Introduction 3.1.2 History 3.2.1 Definitions 3.2.2 Analytic Model 3.2.3 Affine Transformation 3.3.1 Isometry 3.3.2 Model/Collinearity 3.3.3 Model/Isometry 3.4.1 Direct Isometry 3.4.2 Model/Direct 3.5.1 Indirect Isometry 3.5.2 Model/Indirect 3.6.1 Similarity Transformation 3.6.2 Model/Similarity 3.7 Other Affine Transformations

Ch. 4 Projective Geometry Ch. 4 Table of Contents 4.1.1 Introduction 4.1.2 Historical 4.2.1 Axioms 4.2.2 Basic Theorems 4.3 Duality 4.4 Desargue's Theorem 4.5.1 Harmonic Sets 4.5.2 Music & Harmonic Sets 4.6.1 Definitions for Projectivity 4.6.2 Fundamental Theorem 4.6.3 Projectivity/Harmonic Sets 4.6.4 Alternate Construction 4.7.1 Conics 4.7.2 Pascal's Theorem 4.7.3 Tangents to Conics

Other Topics Ch. 5 Spherical Geometry Ch. 6 Fractal Geometry Ch. 7 Topology

Appendices Internet Resources Index Geometer's Sketchpad/GeoGebra JavaSketchpad/GeoGebraHTML Video Lectures Logic Review References Acknowledgements

         4.6.3 Harmonic Sets and Projectivity  Printout
If a man is at once acquainted with the geometrical foundation of things and with their festal splendor, his poetry is exact and his arithmetic musical.
—Ralph Waldo Emerson (1803–1882)

        The Fundamental Theorem of Projective Geometry states that three pairs of corresponding points determine a projectivity between two pencils of points. But, a harmonic set of points consists of four points. Several questions arise.

• Is the projection of a harmonic set, also a harmonic set?
• That is, is a harmonic relationship invariant under a projectivity?
• Does a projectivity exist between two harmonic sets?

In this section, we examine these questions.
        We begin by investigating the first two questions. Since a projectivity is a finite product of elementary correspondences, we first show that an elementary correspondence preserves a harmonic relation.
      Let H(AB,CD) be a harmonic set of points. Let a,b,c,d be a pencil of lines with center E such that E is a point not on AB and a = AE, b = BE, c = CE, d = DE. 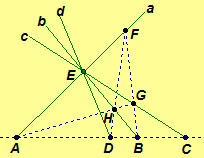Hence, we have an elementary correspondence . We assert that H(ab,cd), a harmonic set of lines.
      Since H(AB,CD), by the constructive proof of Theorem 4.6, there is a complete quadrangle EFGH such that A and B are diagonal points with A = EF · GH, B = FG · EH,  C = GE · AB, and D = FH · AB. We desire a complete quadrilateral such that a and b are diagonal lines and c and d are determined from the third diagonal line. Since FG · FH = F and AH · AB = A are on a, we would have line a as a diagonal line for the complete quadrilateral determined by FG, FH, AH, and AB. (Show this is a complete quadrilateral.) Thus, we have FG · FH = F and AH · AB = A on a, FG · AB = B and FH · AH = H on b, FG · AH = G on c, and FH · AB = D on d. Hence, by definition of a harmonic set of lines, H(ab,cd). Further, by the principle of duality, the converse is also true.
      Therefore, an elementary correspondence maps a harmonic set of points/lines to a harmonic set of lines/points. Since a projectivity is a finite product of elementary correspondences, a projectivity maps a harmonic set to another harmonic set. We have proven that a harmonic relationship is invariant under a projectivity as stated in the following theorem.

Theorem 4.13. If H(AB,CD) and , then H(A'B',C'D').

Exercise 4.36. Show the complete quadrilateral defined by FG, FH, AH, and AB in the above proof is in fact a complete quadrilateral.

The above result, together with the Fundamental Theorem of Projective Geometry and Corollary 4.9, answers our other questions about the relationship between harmonic sets.

Theorem 4.14. There exists a projectivity between any two harmonic sets.

Exercise 4.37. Prove Theorem 4.14.     

If all art aspires to the condition of music, all the sciences aspire to the condition of mathematics.
—George Santayana (1863–1952)