Fraction Basics

Some Basic Fraction Ideas

Proper Fraction

Each of the fractions (in the examples on the previous page) is called a proper fraction since the fraction represents a part of a single whole object. A proper fraction is a fraction in which the numerator is less than the denominator.  For example,  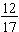is a proper fraction because 12 < 17. 

Improper Fraction

Sometimes we need to write fractions that have more than one whole object.
For example,

each rectangle is a whole divided into four equal parts and the total shaded portions may be written as 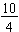. Since the number of equal parts is more than one whole, we call the fraction an improper fraction. An improper fraction is a fraction in which the numerator is greater than or equal to the denominator. For example, 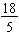 is an improper fraction because 18 > 5.

Denominator of One

Extending the above idea of improper fractions to just whole numbers, we may write every whole number as an improper fraction with a denominator of 1. For example, if each rectangle is a whole consisting of 1 part,

the 3 whole rectangles may be written as the improper fraction 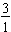. All whole numbers can be written in fractional notation.

Fractional Notation for One

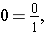
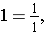
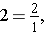
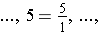
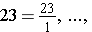
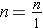
We may write the fractional notation for 1 many different ways as improper fractions.

Examples:
has a shaded portion of 1 part and may be written in fraction form as .
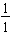 has 4 equal shaded parts and may be written in fraction form as .
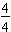There are infinitely many fractional notations for 1.  If we divide an object into n parts and take n of the parts, we obtain all of the object or the whole. 

 

Fractional Notation for Zero

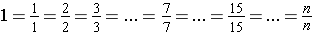
Similarly, there are infinitely many fractional notations for 0. 

Examples:
  has no shaded portions and may be written in fraction form as .
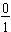has no shaded parts and may be written in fraction form as .
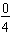If we divide an object into n parts and take none of them, we get 0.

Denominator Is Nonzero

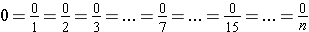
Note that by definition the denominator of a fraction is never zero, that is, 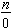is not defined for any whole number n. The reason is that the denominator for common fractions represents the number of equal parts a whole object is divided into and this must be at least one. A whole object cannot be divided into zero parts.

return to top | previous page | next page