Fraction Basics

Equivalent Fractions

 As noted before, there are an infinite number of ways to express the idea of one whole as a fraction.  It turns out that there are an infinite number of ways to express any fractional part.  Fractions that name the same part of the whole are called equivalent fractions.

Example:

Notice that the rectangular strips (wholes) are the same size.  Also notice that the shaded portion is the same size within each strip, and the same fractional part of each strip is shaded. The difference is only in how each shaded region is named. We use an equal sign to denote equivalent fractions. By the above illustration, we have

. 

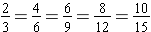Note. The numerators are multiples of 2 and the denominators are multiples of 3.

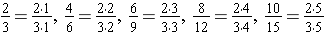
We have modeled the following property:

The Fundamental Law of Fractions Let  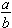be a fraction. Then 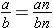, for any nonzero integer n, that is,  is equivalent to any fraction of the form

 

Example:

Notice that the rectangles (wholes) are the same size.  Also notice that the shaded portion is the same size in each, and the same fractional part is shaded in each.  The difference is only in how each shaded region is named.

The Fundamental Law of Fractions states that multiplying both the numerator and denominator of a fraction by the same non-zero whole number produces an equivalent name for the same fractional amount. For this problem, we have

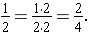
Another way of viewing this result is to remember that is a name for one, so in essence this is multiplying the fraction one-half by one, which gives us an equal amount. The Identity Property for Multiplication tells us that multiplication by one does not change the value of the other factor.

For the same reason, dividing both numerator and denominator by a common factor will also produce an equivalent name for the same fraction because we are essentially dividing by one.  This is called simplifying a fraction.  When one is the only common factor for the numerator and denominator, the fraction is in "simplest form", sometimes called "simplest terms."

Example:

 

return to top | previous page | next page