Fraction Basics

Bar Diagrams

We may use bar diagrams to help solve some types of problems. For example, use a bar diagram to solve the following problem:

Jamie paid Dana three-fourths of the $60 she owed Dana. How much money did Dana receive from Jamie?

A helpful first step in solving a problem of this type is to reword it. With the above example, we are asking the question:

What is 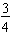of 60?

A helpful way to solve fraction problems like this problem is to use a bar diagram.  A bar is used to represent the whole. So we label it with the amount of the whole.

 

Since the denominator tells us how many equivalent pieces the whole is divided into, we divide the bar into that many equivalent pieces and label each piece with its value.

Finally, we indicate the required number of fractional parts with a question mark and determine the value represented.

Since one unit is 15, three units would be 45.

So, 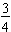of 60 is 45.

Dana received $45 from Jamie.

 When you work a problem you should show your work as above.  We will be building on this method to help better understand multiplication of a fraction and a whole number as well as the multiplication of fractions.

Note that the above problem could be solved by multiplying:

.

 

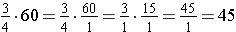return to top | previous page | next page