Fraction Basics

Finding Simplest Form

As in the above examples, simplest form can be achieved by either eliminating all common factors greater than one or by dividing several times until the numerator and denominator have no common factor other than one.

A more efficient way to find the simplest form of a fraction is to use the GCF (greatest common factor) of the numerator and denominator. In the following examples, we illustrate several methods: prime factorization, factor the GCF, and divide both numerator and denominator by the GCF.  

Prime Factorization Method

To use the prime factorization method for finding the simplest form of a fraction, we rewrite the fraction in the form with the prime factorization of the numerator and denominator. Next, rewrite the factorization with the greatest common factor as a separate factor. Finally, apply the Fundamental Theorem of Fractions to write the simplest form.

Example: Find the simplest form for the fraction .

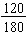We find the prime factorization for the numerator and denominator and then rewrite with the GCF written as a separate factor for the numerator and denominator. Finally, apply the Fundamental Law of Fractions.

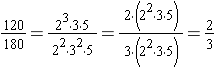
Example: Write the fraction  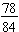in simplest terms.

 

Factor the GCF Method

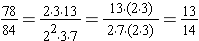
For this method, we first find the greatest common factor for the numerator and denominator. Next, rewrite the numerator and denominator each as two factors where one of the factors is the greatest common factor. Finally, apply the Fundamental Theorem of Fractions to write the simplest form.    

Example: Find the simplest form for the fraction .

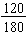We find the greatest common factor for the numerator and the denominator:
120 = 2³ · 3 · 5 and 180 = 2² · 3² · 5 so the GCF(120, 180) = 2² · 3 · 5 = 60.
To simplify 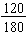, rewrite the fraction in a factored form and apply the Fundamental Law of Fractions.

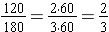
Example:  Write the fraction  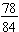in simplest terms.

We find the greatest common factor for the numerator and the denominator:
78 = 2 · 3 · 13 and 84 = 2² · 3 · 7 so the GCF(78, 84) = 2 · 3 = 6.
To simplify 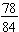, rewrite the fraction in a factored form and apply the Fundamental Law of Fractions.

 

Method of Divide the Numerator and Denominator by the GCF.

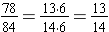
This method is a variation of the previous method where instead of writing the numerator and denominator in a factored form, we divide the numerator and denominator by the greatest common factor.

Example:  Find the simplest form for the fraction .

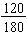We find the greatest common factor for the numerator and the denominator:
120 = 2³ · 3 · 5 and 180 = 2² · 3² · 5 so the GCF(120, 180) = 2² · 3 · 5 = 60.

To simplify 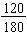completely, divide both numerator and denominator by the 60.

 Example:  Write the fraction  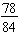in simplest terms.

We find the greatest common factor for the numerator and the denominator:
78 = 2 · 3 · 13 and 84 = 2² · 3 · 7 so the GCF(78, 84) = 2 · 3 = 6.

To simplify 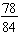completely, divide both numerator and denominator by the 6.

 

return to top | previous page | next page