Laws of Exponents

Scientific Notation

Multiplication of Values with the Same Base

We previously (Session 13) multiplied terms like x² · x³ and 3y² · 7y by applying the definition of exponent.

Example:

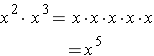
In this case we see that is the base for each of the exponent expressions being multiplied and that we end up with x being used as a factor a total of 2 + 3 = 5 times.

Example:

In this case we see that y is the base for each exponent expression being multiplied and that we end up with y being used as a factor a total of 2 + 1 = 3 times.

Now we develop rules that make these computations shorter and more efficient.

The previous examples above show what happens when we multiply two exponential expressions that have the same base. The fact that the base number is the same allows us to simply sum the number of times the base is used as a factor. It is important to remember that this only happens when the bases are the same.

Two More Motivation Examples:

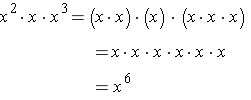
Note that a value with no exponent is the same as having an exponent of one. For example, 5¹ = 5 and x¹ = x.

Now we are ready to formalize what we know about how to multiply variable expressions that have the same base. We see from the examples above that when we multiply exponent expressions that have the same base, we get that base as many times as the sum of the exponents of the base.  

Multiplication of Values with the Same Base. When multiplying two exponential expressions with the same base, the product has the same base with an exponent that is the sum of the exponents of the factors.

General Property:     b^m · bⁿ = b ^{(m + n)}

Examples:  10¹⁹ · 10²³ = 10¹⁹⁺²³ = 10⁴²           3⁷ · 3⁸ = 3⁷⁺⁸ = 3¹⁵

                      y ⁴ · y ⁵ = y ⁴⁺⁵ = y ⁹                         5⁷ · 5 · 5⁶ = 5⁷⁺¹⁺⁶ = 5¹⁴

 Examples with coefficients or more than one variable:

Self-Check Problems

Simplify each expression in terms of the exponents.

107 · 1014	Solution
m4 · m5	Solution
7ab2 · 9a3b7	Solution

return to top | previous page | next page