Laws of Exponents

Scientific Notation

Division of Values with the Same Base

Two Motivation Examples:  

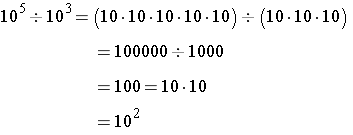  or

 

  or

Note that the exponent in the quotient is the difference between the exponents in the dividend and divisor.

Division of Values with the Same Base. When dividing two exponential expressions with the same base, the quotient has the same base with an exponent that is the difference between the exponents of the dividend and divisor.

General Property: b^m ÷ bⁿ = b ^{(m – n)} or 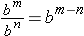where m ≥ n and b ≠ 0.

(In Session 41, we will extend this property to values with m < n.)

Examples: 10²³ ÷ 10¹⁹ = 10^23–19 = 10⁴             3⁸ ÷ 3⁷ = 3^8–7 = 3¹ = 3

                  y ⁹ ÷ y ³ = y ^9–3 = y ⁶                        5⁸ ÷ 5⁶ = 5^8–6 = 5²

Since we are only using whole numbers at this time, we require that the first term have an exponent of greater value that the second term. This property will be generalized later in the course after we have introduced integers.

Self-Check Problem

Simplify each expression in terms of the exponents.

	Solution
	Solution
	Solution

 

return to top | previous page | next page