Laws of Exponents

Scientific Notation

Exponential Expression Raised to a Power

Likewise, we have previously been simplifying variable expressions like (3x)² and (2x²y)³ by applying the definition of exponent.

.Example:  

In this case we see that when the product (3x) is raised to the second power, it comes out the same as a raising each factor to the second power.

Example:

In this case we see that when the product (2x²y) is raised to the third power, it is the same as raising each factor to the third power.

Two Basic Examples using the Rule for Multiplication with the Same Base:

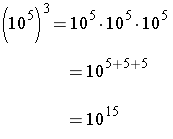
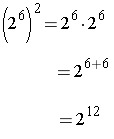
Note that the exponent in the result is the product of the exponents in the original expression.

Raising an Exponential Expression to a Power. When an exponential expression is raised to a power, the result has the same base with an exponent that is the product of the exponents.

General Property:  (b^m)ⁿ = b^mn

Examples:  (10³)⁹ = 10³⁽⁹⁾ = 10²⁷

   (3⁸)⁷ = 3⁸⁽⁷⁾ = 3⁵⁶

(y ⁹)³ = y ⁹⁽³⁾ = y ²⁷

  (5⁸)⁶ = 5⁸⁽⁶⁾ = 5⁴⁸

Self-Check Problem

Simplify in terms of the exponents

(107)8	Solution
(d9)6	Solution

return to top | previous page | next page